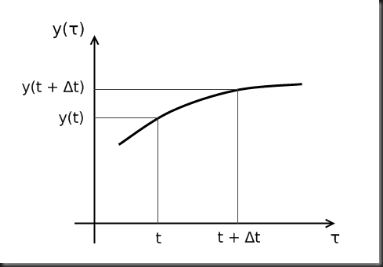
Let a function y(τ) and two time points: t and t + Δt.
We will now make an approximation by saying that if Δt is small enough, y(τ) is approximately constant over the interval [t, t + Δt] and equal to the average of y(t) and
y(t + Δt).
Based on this approximation, the integral of y(τ) over the interval [t, t + Δt] is given by
The previous equation is the integral form of the trapezoidal rule, we will now derive the differential form which will be used in the next posts.
Let
Substituting in the integral form of the trapezoidal rule

The previous equation is the differential form of the trapezoidal rule. It will be used to replace the differential equations that appear in circuits containing energy storage elements by algebraic equations.
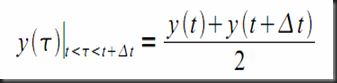

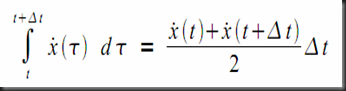

No comments:
Post a Comment