The Capacitor’s Companion Model
At any point in time, the equation relating the capacitor voltage to the capacitor current is
This equation is not very useful because it will cause terms with to appear in the Modified Nodal Analysis (MNA) equations. We do not have a computer method for solving sets of linear differential equations. We can only solve sets of linear algebraic equations (remember the triangular decomposition algorithm and our LinearEquations class).
We will combine the trapezoidal rule with the capacitor’s differential equation to get a linear algebraic equation relating the capacitor voltage to the capacitor current.
The differential form of the trapezoidal rule is

We will now replace the generic variable (x) by the voltage across the capacitor (v).
Substituting into the trapezoidal rule equation
Equation (1) says that the relation between the capacitor voltage and the capacitor current at time t + Δt depends on the capacitor voltage and the capacitor current at time t. This means that the capacitor (like other energy storage elements as we will see later) has memory.
Two circuits that satisfy equation (1) are shown in the following figure.
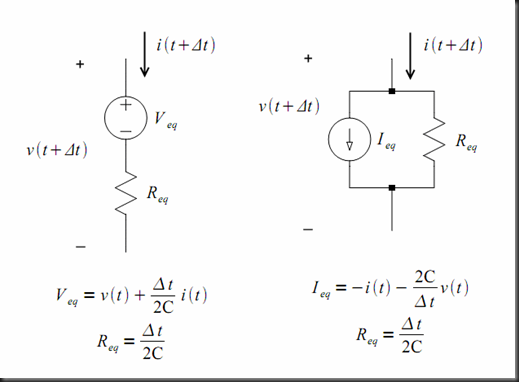
These equivalent circuits are called companion models.
The solution at time t is used to build the companion models that will be used to solve the circuit at time t + Δt. After building the companion models, DC analysis is performed to get the solution at time t + Δt. The time is then advanced again and the solution at t + Δt is used to build the companion models for the next time point.
The first transient step depends on the initial conditions to build its companion models. The initial conditions can be specified by the user. The unspecified initial conditions are obtained from DC analysis performed prior to transient analysis.
The Inductor’s Companion Model

At any instant, the inductor I-V relationship is given by

This time we substitute x by the capacitor current (i).
Substituting in the trapezoidal rule

The two companion models that satisfy equation (2) are shown in the figure below.
The Transformer’s Companion Model
I could not find the transformer’s companion model anywhere, so I derived it myself.

The transformer’s time domain equations are

Again, we will write the differential form of the trapezoidal rule.

Substituting in the trapezoidal rule equation we get
Rearranging

Substituting in the trapezoidal rule equation we get

A companion model that satisfies equations (3) and (4) is shown in the figure below.
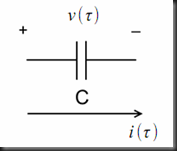
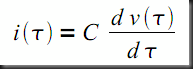







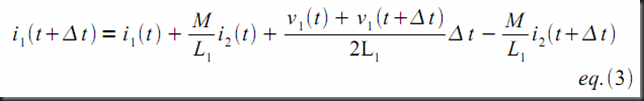


No comments:
Post a Comment