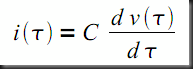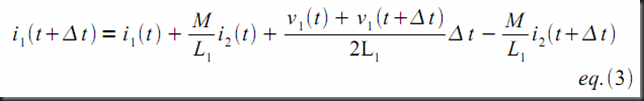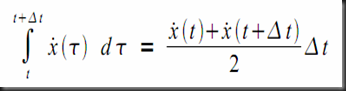Automatic Step Size Control

The trapezoidal rule we used to derive the companion models involves some degree of approximation. The error due to this approximation depends on, among other uncontrollable things, the step size (Δt). Reducing the step size will generally enhance the accuracy, but will cause the simulation to take longer because a larger number of solutions will be needed to get to the user specified final time. We want the largest step size that still gives an acceptable accuracy. The problem now becomes: how to estimate the error for a certain step size?

Before answering this question, we need to distinguish between local error and global error (or cumulative error).
The local error includes only the error incurred in the present time step, unlike global error which includes the error due to the starting point of the present time step being inexact. The global error contains the cumulative effect of local errors in all previous steps.
The global error is of high interest but unfortunately only the local error can be estimated.

I will now present the local error estimation method. I will start by rewriting the differential form of the trapezoidal rule using a slightly different notation.

 
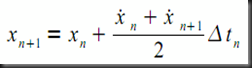
'n' is the step index and Δt_n is the difference between the time of step n+1 and the time of step n.
The local error incurred due to the approximation of the trapezoidal rule while moving from solution n to solution n+1 is approximately given by

where 

The third derivative of x can be approximated by the third divided difference of x on the nodes t_n+1, t_n, t_n-1, t_n-2. And here is how to get the divided difference.

This means that you need the solution at the time points t_n-2, t_n-1, t_n, t_n+1 to estimate the local error incurred while moving from t_n to t_n+1. If the error is not acceptable, you will have to discard the solution at t_n+1 and try again with a smaller step size.

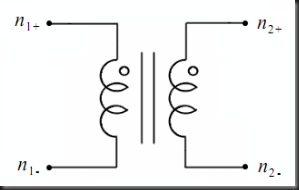
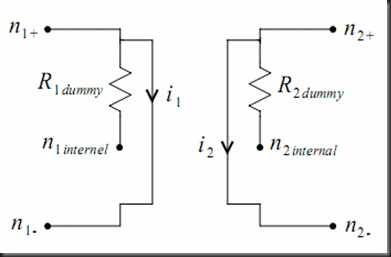
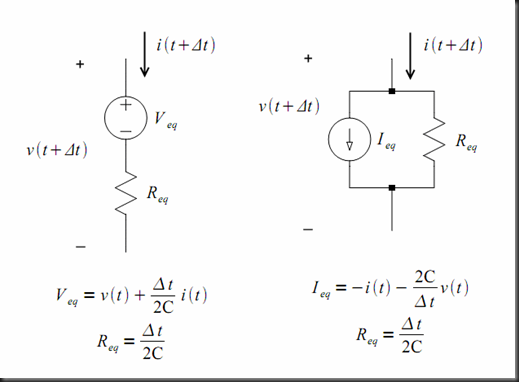
The variable x used in the previous equations represents the voltage across capacitors, the current through inductors and, for transformers, x represents the expressions shown below.

 
The local error should be calculated independently for each energy storage element in the circuit after each solution and if the error at one energy storage element is not acceptable, the solution is discarded and the step size is reduced.

It remains to say that the local error due to the approximation of the trapezoidal rule is called the Local Truncation Error and abbreviated LTE.

Energy Storage Element Stamps for Transient Analysis

As was mentioned before, a DC analysis is performed prior to transient analysis to get the solution at t = 0. During this DC analysis, coils and capacitors for which no initial conditions were specified are replaced by short circuits and open circuits respectively, while coils and capacitors for which initial conditions were specified, are replaced by infinite-impedance current sources and zero-impedance voltage sources respectively.
Also, at each time point after t = 0, each energy storage element is replaced by its companion model.

This means that, to perform transient analysis, three matrix stamps are needed for each energy storage element:

1. A stamp to be used at t = 0 if no initial condition is specified.
2. A stamp to be used at t = 0 if an initial condition is specified.
3. A stamp to be used at t > 0.

I found that the computer implementation of transient analysis will be greatly simplified if

1. The three stamps for an energy storage element have the same size.
2. The index of an excess unknown points to the same excess unknown in the three stamps.

We should have these two conditions in mind while choosing the equivalent circuits for energy storage elements.

The Capacitor Stamps

1) At t = 0 / no IC specified

 
The dashed line in the figure above separates the node equations from the excess equations, and the node voltages from the excess unknowns.

2) At t = 0 / IC specified

The dummy resistor between node plus and the internal node is added just to make the coefficients matrix nonsingular.

3) At t > 0

  
Note that in the three cases the stamp has a the same size, the first excess unknown index points to the internal node voltage, and the second excess unknown index points to the capacitor current. So the two conditions stated above are satisfied.

The Inductor Stamps

 
1) At t = 0 / no IC specified

  
2) At t = 0 / IC specified

3) At t > 0

  

The Transformer Stamps

 
1) At t = 0 / no IC specified

 
Stamp of the primary coil

Stamp of the secondary coil

2) At t = 0 / IC specified

 
Stamp of the primary coil

 
Stamp of the secondary coil

 
In the previous two cases, I gave two separate stamps for the primary and the secondary rather than one big stamp for both of them because the user may specify an initial condition for one coil and leave the initial condition for the other coil unspecified.

3) At t > 0

What Makes a Circuit Element an Energy Storage Element?

The constitutive equation of a circuit element is a relationship imposed by the element on the solution of the circuit.

If the constitutive equation of an element does not depend on the state of the element at previous time points, then this element is a memoryless element. For example the constitutive equation of a resistor at time t is v(t) = i(t) * R. This is clearly independent of the voltage across and the current through the resistor at any time before t. This makes the capacitor a memoryless element.

Conversely, if the constitutive equation of an element does depend on the state of he element at a previous time point, then the element is an energy storage element and does have memory. Equations (1), (2), (3) and (4) in the previous post show that the inductor, the capacitor, and the transformer are energy storage elements because their constitutive equations at time t + 1 depend on their state at time t.

Companion Models

The Capacitor’s Companion Model

At any point in time, the equation relating the capacitor voltage to the capacitor current is

This equation is not very useful because it will cause terms with to appear in the Modified Nodal Analysis (MNA) equations. We do not have a computer method for solving sets of linear differential equations. We can only solve sets of linear algebraic equations (remember the triangular decomposition algorithm and our LinearEquations class).

We will combine the trapezoidal rule with the capacitor’s differential equation to get a linear algebraic equation relating the capacitor voltage to the capacitor current.
The differential form of the trapezoidal rule is

We will now replace the generic variable (x) by the voltage across the capacitor (v).

Substituting into the trapezoidal rule equation

Equation (1) says that the relation between the capacitor voltage and the capacitor current at time t + Δt depends on the capacitor voltage and the capacitor current at time t. This means that the capacitor (like other energy storage elements as we will see later) has memory.

Two circuits that satisfy equation (1) are shown in the following figure.

These equivalent circuits are called companion models.

The solution at time t is used to build the companion models that will be used to solve the circuit at time t + Δt. After building the companion models, DC analysis is performed to get the solution at time t + Δt. The time is then advanced again and the solution at t + Δt is used to build the companion models for the next time point.
The first transient step depends on the initial conditions to build its companion models. The initial conditions can be specified by the user. The unspecified initial conditions are obtained from DC analysis performed prior to transient analysis.

The Inductor’s Companion Model

At any instant, the inductor I-V relationship is given by

Remember the trapezoidal rule

This time we substitute x by the capacitor current (i).

Substituting in the trapezoidal rule

The two companion models that satisfy equation (2) are shown in the figure below.

The Transformer’s Companion Model

I could not find the transformer’s companion model anywhere, so I derived it myself.

The transformer’s time domain equations are

Again, we will write the differential form of the trapezoidal rule.

First let

Substituting in the trapezoidal rule equation we get

Rearranging

Now let

Substituting in the trapezoidal rule equation we get

Rearranging

A companion model that satisfies equations (3) and (4) is shown in the figure below.

The Trapezoidal Rule

Let a function y(τ) and two time points: t and t + Δt.

We will now make an approximation by saying that if Δt is small enough, y(τ) is approximately constant over the interval [t, t + Δt] and equal to the average of y(t) and
y(t + Δt).

Based on this approximation, the integral of y(τ) over the interval [t, t + Δt] is given by

The previous equation is the integral form of the trapezoidal rule, we will now derive the differential form which will be used in the next posts.

Let

 

Substituting in the integral form of the trapezoidal rule

  
Rearranging

The previous equation is the differential form of the trapezoidal rule. It will be used to replace the differential equations that appear in circuits containing energy storage elements by algebraic equations.