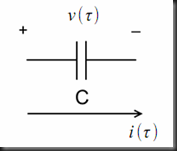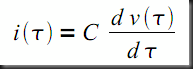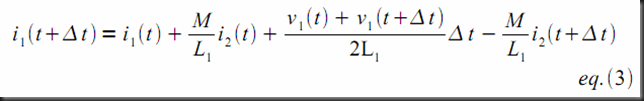Companion Models

The Capacitor’s Companion Model

At any point in time, the equation relating the capacitor voltage to the capacitor current is

This equation is not very useful because it will cause terms with to appear in the Modified Nodal Analysis (MNA) equations. We do not have a computer method for solving sets of linear differential equations. We can only solve sets of linear algebraic equations (remember the triangular decomposition algorithm and our LinearEquations class).

We will combine the trapezoidal rule with the capacitor’s differential equation to get a linear algebraic equation relating the capacitor voltage to the capacitor current.
The differential form of the trapezoidal rule is

We will now replace the generic variable (x) by the voltage across the capacitor (v).

Substituting into the trapezoidal rule equation

Equation (1) says that the relation between the capacitor voltage and the capacitor current at time t + Δt depends on the capacitor voltage and the capacitor current at time t. This means that the capacitor (like other energy storage elements as we will see later) has memory.

Two circuits that satisfy equation (1) are shown in the following figure.

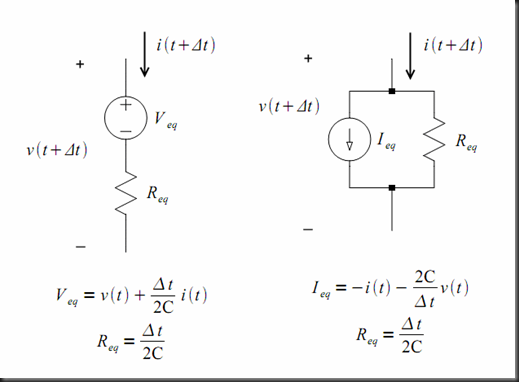
These equivalent circuits are called companion models.

The solution at time t is used to build the companion models that will be used to solve the circuit at time t + Δt. After building the companion models, DC analysis is performed to get the solution at time t + Δt. The time is then advanced again and the solution at t + Δt is used to build the companion models for the next time point.
The first transient step depends on the initial conditions to build its companion models. The initial conditions can be specified by the user. The unspecified initial conditions are obtained from DC analysis performed prior to transient analysis.

The Inductor’s Companion Model

At any instant, the inductor I-V relationship is given by

Remember the trapezoidal rule

This time we substitute x by the capacitor current (i).

Substituting in the trapezoidal rule

The two companion models that satisfy equation (2) are shown in the figure below.

The Transformer’s Companion Model

I could not find the transformer’s companion model anywhere, so I derived it myself.

The transformer’s time domain equations are

Again, we will write the differential form of the trapezoidal rule.

First let

Substituting in the trapezoidal rule equation we get

Rearranging

Now let

Substituting in the trapezoidal rule equation we get

Rearranging

A companion model that satisfies equations (3) and (4) is shown in the figure below.

What is Linear Transient Analysis?

Transient analysis is used to examine the response of the circuit as a function of time.
Generally, transient analysis can only be applied to circuits that are “lumped” and “time-invariant”.
Lumped means that the circuit is physically small enough to allow us to assume that electric signals affect every point in the circuit simultaneously.
Time-invariant means that delaying the input signal by a certain time simply delays the response by the same time.
The two previous definitions are from the book “Electric Circuits” by James W. Nilson.

Linear transient analysis is a special case of transient analysis where the circuit to be analyzed may only contain linear elements.

In the context of transient analysis, a two-terminal element is linear if the relationship between the instantaneous voltage across the element and the instantaneous current through the element can be described by a linear (differential) equation.
The following figure shows that the resistor, the inductor, and the capacitor are all linear elements.

For elements having more than two terminals, an element is linear if the relationships between instantaneous currents and/or instantaneous voltages imposed by the element can be described by a set of linear (differential) equations.
The following figure shows that the current controlled voltage source and the transformer are linear elements.

To conclude, linear transient analysis is used to examine the response of a linear, lumped, time-invariant circuit as a function of time.

Initial Conditions

The solution of the circuit at t = 0 must be known before performing transient analysis because the time domain solution of a circuit depends on the initial state of the energy storage elements in the circuit and also because the user may be interested in the values of some circuit variables at t = 0.

DC analysis is performed prior to transient analysis to get the initial transient solution which is the solution at t = 0.
The user may be given the option to specify initial conditions on energy storage elements (initial currents through coils and initial voltages across capacitors). In this case, the user specified initial conditions are used as constraints on the initial transient solution. Specifically, during the DC analysis, coils and capacitors for which no initial conditions were specified are treated as short circuits and open circuits respectively, and coils and capacitors for which initial conditions were specified are treated as infinite-impedance current sources and zero-impedance voltage sources respectively.

The next version of the simulator will be called Soft Analyst and will support transient analysis.